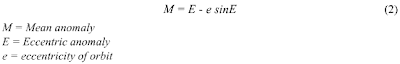The Night Sky in May

From the Night sky Newsletter:

The Night Sky This Month (May 2010)




Learn more! Visit NightSkyInfo.com (http://www.nightskyinfo.com).



You are receiving this message because you visited us at

http://www.nightskyinfo.com and registered to receive our monthly

newsletter. If you feel you have received this issue in error, please

follow the instructions at the end of the page to unsubscribe.



Key Stars



From mid-northern latitudes, Arcturus (Alpha Bootis) blazes high overhead,

while Spica (Alpha Virginis) shines in the south. Castor (Alpha Geminorum)

and Pollux (Beta Geminorum) are sinking towards the western horizon,

followed by Regulus (Alpha Leonis) and the stars of Leo. In the east, the

stars of the Summer Triangle, led by Vega (Alpha Lyrae), are rising.

Antares (Alpha Scorpii) is climbing into view in the southeast, although is

still low on the horizon.



The Planets



Mercury



During the last two weeks of May, you should be able to spot Mercury very

low in the east 30 minutes before sunrise. The planet reaches greatest

elongation (25.1 degrees west of the Sun) on May 26. This is also about

when it is highest for mid-northern observers.



Venus



Venus is the bright "Evening Star", blazing in the west after dusk. In

early May, Venus' disk spans 11" across and is 88-percent lit. By late in

the month, the disk has grown to 13" and the phase has shrunk to 81-percent

illumination.



Mars



Mars can be found after sunset in the southwestern sky, between the figures

of Cancer the Crab and Leo the Lion. It shines at magnitude +1 this month,

and its 7"-diameter disk reveals practically no detail through a telescope.





Jupiter



Jupiter was in conjunction with the Sun on February 28; now it slowly

emerges into dawn view. You can find it above the eastern horizon, about 30

minutes before sunup.



Saturn



This month Saturn remains visible nearly all night. Look for it high in the

south after sunset, just a couple of degrees below Denebola, the second

brightest star in the constellation Leo the Lion. In a telescope Saturn's

disk spans 19" across the equator and the rings appear very narrow. They

are currently tipped just 1.7 degrees to our line of sight, but after the

end of the month they will begin to widen again.



Uranus



The seventh planet is in the morning sky, in the same binocular field as

Jupiter. Uranus glows at magnitude +5.9 and its disk (3.6" across) shows up

readily in the smallest telescope.



Neptune



Neptune lies in western Aquarius, a region that stands 25 degrees high in

the southeast when morning twilight begins. Neptune shines at magnitude

+7.9, so you will need a telescope to spot it.



Pluto



Pluto, magnitude +14, lies in northwestern Sagittarius and is highest above

the horizon in the predawn sky. It can only be viewed in larger amateur

telescopes.



Bright Asteroids



Vesta



7th-magnitude Vesta is an easy find in binoculars. Look for it just after

dusk, when Leo the Lion - the constellation through which the asteroid

tracks - is highest above the southwestern horizon.



Ceres



This month, Ceres arcs through the rich star fields of northern

Sagittarius. Glowing at 8th magnitude, Ceres shows up through binoculars

under a dark sky, but you will need a scope to follow it from the suburbs.



Pallas



Pallas shines at magnitude +9 and lies in the constellation Corona Borealis

the Northern Crown. Look around midnight, when the asteroid reaches its

highest altitude.



Bright Comets



C/2009 K5 McNaught



Comet C/2009 K5 McNaught sweeps from Cepheus past Polaris to Camelopardalis

during the month and remains circumpolar (meaning it never sets) for most

mid-northern observers. It glows with the combined light of a 9th-magnitude

star, easily accessible from suburban backyards with a 4-inch scope.



81P Wild



This periodic comet glows around 10th magnitude and lies within a few

degrees of the 4th-magnitude star Iota Virginis all month. At 10th

magnitude, Wild will be as tough to view as the faintest Messier galaxies

in Virgo.



Meteor Showers



The Eta Aquarids radiate from a point in northern Aquarius, close to Eta

Aquarii. Eta Aquarid meteors first appear around April 28, and some can be

seen until May 21. The shower's peak occurs around May 7, when up to 20 or

30 meteors can be seen each hour from a dark-sky site. Before and after the

maximum, the Eta Aquarids produce only two or three meteors per hour.



Sky Events



May 2 - Venus is 6.4 degrees north of Aldebaran (Alpha Tauri) at 9:56 P.M.

EDT.



May 6 - Last Quarter Moon at 12:15 A.M. EDT. The Moon is at apogee, the

point in its orbit when it is farthest from Earth.



May 7 - The Eta Aquarid meteor shower reaches maximum activity.



May 13 - New Moon at 9:04 P.M. EDT.



May 16 - The Moon is 0.1 degree south of Venus at 6:16 A.M. EDT.



May 19 - The Moon is 4 degrees south of the Beehive cluster (M44) in Cancer

at 7:03 A.M. EDT.



May 20 - First Quarter Moon at 7:43 P.M. EDT. The Moon is at perigee, the

point in its orbit when it is nearest to Earth.



May 26 - Mercury is at greatest western elongation, 25.1 degrees west of

the Sun in the morning sky.



May 27 - Full Moon at 7:07 P.M. EDT.



May 28 - The Moon is 1.9 degrees north of Antares (Alpha Scorpii) at 12:30

A.M. EDT.



May 29 - The Moon is 0.1 degree south of the dwarf planet Ceres at 5 P.M.

EDT.




Copyright © 1994-2010 Yahoo! Inc. All rights reserved. Terms of Service - Copyright/IP Policy - Guidelines

Asteroid in Near-Earth Pass

Potentially Dangerous Asteroid Spotted Passing Earth


By SPACE.com Staff



posted: 29 April 2010

11:12 am ET



An asteroid on the list of potentially dangerous space rocks that could endanger the Earth was caught on camera as it zoomed past our planet this month, and found to be larger than astronomers originally thought.



The asteroid buzzed the Earth on April 19 and came within 1.5 million miles (2.4 million km) of the planet. That's about six times the distance between Earth and the moon.



Astronomers used the planetary radar system on the famed Arecibo radio telescope in Arecibo, Puerto Rico to spot the asteroid, called 2005 YU55, over four days starting on April 19. The photo revealed the asteroid as a half-lit space rock flying through the solar system.



Ads by GoogleHam radio w/o Morse codeFCC dropped Morse code requirement! Ham license in 10 hours study.

www.hamtestonline.comEarth Day ActivitiesLearn How Ford's Green Technology is Showing the Earth Lots of Love.

TheFordStory.comOwn Saving Private RyanSee this Oscar Winning Spielberg Film, New to Blu-ray. Pre-Order Now

www.amazon.com/Saving-Private"This object is on the list of 'potentially hazardous asteroids' maintained by the Minor Planet Center, of the Harvard-Smithsonian Center for Astrophysics, Cambridge, Mass.," Arecibo astronomers said in a statement. [More asteroid photos.]



The astronomers found that the asteroid is about 1,300 feet (400 meters) in size – about a quarter-mile (400 meters) long and twice as big as originally thought. The Arecibo telescope's planetary radar system resolved features on the asteroid down to about 25 feet (7.5 meters).



Asteroid 2005 YU55 was first discovered by astronomer Robert McMillan, of the Spacewatch detection team, on Dec. 28, 2005. And this isn't the only chance astronomers will have to study 2005 YU55.



The space rock will be back.



On Nov. 8, 2011, the asteroid will complete another trip around the sun and swing by Earth again just inside the moon's orbit. It should fly by at a distance of 191,120 miles (307,577 km), about eight-tenths the distance between Earth and the moon. The distance from Earth to the moon is on average about 238,900 miles (384,472 km).



The asteroid poses no risk of impacting the Earth when it returns next year, though astronomers will keep watching its path through space.



NASA routinely tracks asteroids and comets that may fly near the Earth with a network of telescopes on the ground and in space. The agency's Near-Earth Object Observations program is responsible for finding potentially dangerous asteroids and studying their orbits to determine if they pose a risk of hitting the Earth.



So far, the program has found about 85 percent of the huge asteroids that fly near Earth, but it hasn't been quite as good at finding rocks that are smaller. The program detected only 15 percent of space rocks that are 460-feet (140-meters) wide and could potentially cause widespread devastation at their impact sites if they hit us, according to a recent report by the National Academy of Sciences.



Only 5 percent of asteroids 164-feet (50-meters) across have been found, the report found. More funding is needed if NASA hopes to reach a Congress-mandated goal of tracking all potentially dangerous space rocks.



President Barack Obama has proposed a budget increase in NASA's asteroid-tracking program that would boost its resources from $3.7 million in 2009 to $20.3 million in 2011. The program received a $2 million increase in 2010 to support the Arecibo telescope.



Obama has also proposed sending astronauts to visit an asteroid by 2025 to study it and gather data that could help astronomers find ways to deflect space rocks before they threaten all life on Earth.



The Arecibo Observatory is part of the National Astronomy and Ionosphere Center which is managed by Cornell University under a deal with the National Science Foundation. Astronomers with Cornell, NASA's Jet Propulsion Laboratory, California Institute of Technology and the University of Maine participated in the observing of asteroid 2005 YU55.

Our Universe Was Born in a Black Hole

This articles originally appeared on Space,com

Yahoo! Buzz

Our Universe Was Born in a Black Hole, Theory Says

By Charles Q. Choi

SPACE.com Contributor

posted: 27 April 2010

08:08 am ET



Our universe might have originated from a black hole that lies within another universe.



The idea centers on how matter and energy falling into a black hole could in theory come out a "white hole" in another universe. In such a situation, both the black hole and the white hole are mouths of an Einstein-Rosen bridge, popularly known as a wormhole.



With that in mind, theoretical physicist Nikodem Poplawski at Indiana University conjectured that when a black hole forms upon the collapse of a dying star, a universe is born at the same time from the white hole on the other side of the wormhole.



Ads by GoogleThe Universe at HISTORY™Watch Videos About Our Mysterious & Expanding Universe Online Now.

History.comThe God Who Wasn't There"Makes the case that Jesus Christ never existed" -Newsweek. Buy DVD.

www.TheGodMovie.comBlood Pressure DiscoveryHugh Downs Reports: Artery clearing secret from Nobel Prize Winner

www.bottomlinesecrets.com"Our universe could have itself formed from inside a black hole existing inside another universe," he said.



This idea has been suggested before, and now Poplawski has expanded on the thinking.



Nested universes



Although a black hole forming from a star the size of our sun would only be about 2 miles wide, it does not mean that a universe which might originate from a black hole would stay that small.



"Our universe was small a long time ago and expanded," Poplawski said. "From the other side, one would not see our expansion." Essentially, a black hole could seem bigger on the "inside" than how it looked to someone outside.



If anyone survived a trip into a black hole and emerged in another universe, "it would be a one-way trip," Poplawski noted. The event horizon of a black hole is boundary at which nothing inside can escape.



In theory, black holes do lose mass, however, as Hawking radiation — particles that emerge from the vacuum right next to their event horizons. Black holes that lose more mass than they gain are expected to shrink and ultimately vanish. This does not mean any universe at the other end of the black hole would cease to exist, Poplawski explained. "We would just be disconnected from the other universe," he said.



Evidence for a black hole birth?



If our universe was born from a black hole in another universe, it would be impossible to cross its event boundary and see the other side, meaning one cannot prove or disprove this idea that way.



So how might one test this conjecture? One implication of Poplawski's concept is that our universe is "closed."



"In cosmology, there are three models for our universe," Poplawski explained. "The first is that it's closed, the second is that it's 'open,' and the third is that it's 'flat.'"



If it is closed, and one tries to venture to the edge of our universe, one would eventually loop back to where one started. "It would be like walking on the surface of the Earth — if you walk to the east, at some point you come back across the west," Poplawski said.



If our universe is flat, and one tries to venture to its edge, one would never reach it, as it continued on infinitely. The same would hold true if the universe is open, "only it would be 'curved,'" Poplawski said. This means that if two beams of light were shot into space parallel to each other, in a flat universe they would stay parallel, while in an open universe they would actually get farther from each other.



If our universe lies "within" another universe, "the prediction would be that our universe is closed," Poplawski said. "That could maybe tested at some point. If the universe is closed, if one watches the stars, their light would be visible on the opposite side of the sky. If the universe is really big, the light from those stars might not have had time to do that yet, but maybe at some point we could see this."



Also, black holes rotate, evidence suggests, and if our universe's parent black hole was spinning, "then one direction might be preferred in our universe, evidence we could see at large scales," Poplawski said.



Solving mysteries?



If our universe was born from a black hole, it could help solve the mystery of what came before the Big Bang and whether our universe was closed, flat or open.



It could also help scientists avoid problems associated with singularities, or infinitely small points with infinite density. In theory, the universe was born from a singularity, and every black hole encloses a singularity. However, singularities are big headaches for theoretical physicists, since the laws of physics break down around them.



"In my model, when the universe is born, there is no problem of having a singularity initially — instead of being infinitely small, it had the radius of its parent black hole," Poplawski said. "Also, instead of black holes ending up with singularities, this model suggests they would end up with universes."



An idea full of holes?



One hole in this idea is one that turns up whenever wormholes are discussed — exotic matter.



In principle, all wormholes are unstable, closing the instant they open. The only way to keep them open is with an exotic form of matter with so-called "negative energy density." Such exotic matter has bizarre properties, including moving in the opposite direction of normal matter when pushed. No one knows if such matter actually exists.



"It is possible that when black holes form, matter can undergo a phase transition to become exotic matter, to allow this initial expansion of a universe inside the black hole," Poplawski suggested.



Also, while this might explain how our universe was born from a black hole, it does not explain how the universe that black hole is from came to be. "So was that universe born from a black hole in another universe, and so on?" Poplawski noted. "It's a problem of an infinite number of universes. That's a very reasonable criticism."



Poplawski will detail his research April 12 in the journal edition of Physics Letters B.



The Strangest Things in Space



The Big Bang: Solid Theory, But Mysteries Remain



The Black Hole That Made You Possible

This article is from space.com


An active star-formation region in the Orion nebula, as seen by Planck. This image covers a region of 13x13 degrees. It is a three-color combination constructed from three of Planck's nine frequency channels: 30, 353 and 857 GHz. Credit: ESA/LFI & HFI Consortia

A low activity, star-formation region in the constellation Perseus, as seen with Planck. This image covers a region of 30x30 degrees. It is a three-color combination constructed from three of Planck's nine frequency channels: 30, 353 and 857 GHz. Credit: ESA/LFI & HFI Consortia

The region of sky covered by the Planck images is shown on a view of half the sky as seen in visible and infrared light. The smaller patch corresponds to Orion and the larger to Perseus. Credit: ESA/LFI & HFI Consortia/STScI DSS

Yahoo! Buzz

Star-Formation Details Seen in New Images

By SPACE.com Staff



posted: 27 April 2010

01:50 pm ET



New images from a European space telescope have revealed a stunning glimpse into the forces driving star formation in our galaxy.



The images were taken from the European Space Agency's (ESA) Planck space observatory and give astronomers a new view into the complex physics that shape the dust and gas in our Milky Way.



In these new images, Planck probed two relatively nearby star-forming regions within our galaxy.



Ads by GoogleHam Radio CoursesPowerful study method. Proven track record. We guarantee you pass!

www.hamtestonline.comThe Universe at HISTORY™Unravel the Secrets of a 13 Billion Year History-Watch Videos Online.

History.comCoffee Fool BannedGrocery stores won't stock us because we're the truth on fresh!

www.CoffeeFool.comPlanck's first new image reveals much of the constellation of Orion, home to the well-known Orion nebula that appears as a bright spot to the lower center of the view. The Horsehead nebula, so-called because at high magnifications its pillar of dust resembles a horse's head, stands out just right of the photo's center.



The Orion region is a cradle of star formation, some 1,500 light-years away. It is famous for the Orion nebula, which can be seen by the naked eye as a faint smudge of pink.



The giant red arc of Barnard's Loop is believed to be the blast wave from a star that exploded in the Orion region approximately 2 million years ago. The bubble it created now stretches about 300 light-years across.



In contrast to Orion,the Perseus region is a less vigorous star-forming area, but there was still plenty for Planck to observe.



"Because Planck is mapping the whole sky, we can capture mosaics of huge regions of the Milky Way," said Charles Lawrence, the NASA project scientist for Planck at NASA's Jet Propulsion Laboratory in Pasadena, Calif. "We are seeing the coldest material in star-forming regions, where stars are at the very earliest stages of formation."



Stars typically form in cosmic nurseries hidden behind veils of interstellar dust. But the Planck observatory scans the universe at long microwave wavelengths, allowing it to peer through the dust at the newborn stars, as well as study the background radiation of the universe.



The images show three physical processes taking place in the dust and gas of the interstellar medium. Planck has the ability to show each process separately by observing them at different frequencies.



At the lowest frequencies, Planck maps emission caused by high-speed electrons interacting with the galaxy's magnetic fields. Planck can also pick up on spinning dust particles emitting at these frequencies.



At intermediate wavelengths, the emission is primarily from gas heated by newly-formed hot stars.



At higher frequencies, Planck maps the sparse amount of heat given out by extremely cold dust. This can reveal the coldest cores in the clouds, which are approaching the final stages of collapse, before they are reborn as full-fledged stars. These stars then disperse the surrounding clouds.



The delicate balance between cloud collapse and dispersion regulates the number of stars that the galaxy makes. Planck observations will help advance researchers' understanding of this interplay, since it can provide data on several major emission mechanisms at the same time.



The Planck observatory launched into orbit in 2009. It's main mission is dedicated to observing the entire sky at microwave wavelengths in order to map the variations in the ancient radiation left over from the Big Bang that was thought to have started the universe about 13.7 billion years ago.



Spectacular Nebulas in Deep Space

Top 10 Star Mysteries

Images – Constellations of the Stars

Cassini reaches Enceladus (Moon of Saturn)

This article is from Space.com

Yahoo! Buzz


Cassini Spacecraft to Glide Over Icy Saturn Moon

By SPACE.com Staff



posted: 27 April 2010

05:15 pm ET



The Cassini spacecraft exploring Saturn will get a new taste of the ringed planet's moon Enceladus late Tuesday when it flies over the icy satellite in a gravity experiment.



NASA's Cassini probe will glide low over Enceladus tonight to perform an experiment designed to probe the moon's interior composition. At closest approach, Cassini will be flying just 60 miles (100 km) above the surface of Enceladus at a speed of 15,000 mph relative to the moon.



The flyby, which will take Cassini through the water-rich plume flaring out from Enceladus' south polar region, will occur on April 27 at 8:10:17 p.m. EDT (0010:17 GMT on April 28).



Ads by GoogleBlood Pressure DiscoveryHugh Downs Reports: Artery clearing secret from Nobel Prize Winner

www.bottomlinesecrets.comThe Universe at HISTORY™Explore Our Mysterious Universe. Videos on Planets, Stars & More.

History.comFree Space WallpapersGet Cool Planet, Star & Moon Wallpapers & Screensavers-Try Them!

Wallpapers.Smileycentral.comScientists plan to use Cassini's radio science instrument to measure the gravitational pull of Enceladus against the steady radio link to NASA's Deep Space Network here on Earth. Detecting any changes will help scientists understand what lies beneath Enceladus' famous "tiger stripe" fractures, which spew water vapor and organic particles from the moon's south polar region.



The experiment is also expected to help scientists learn if the south polar region's sub-surface resembles a lava lamp. Scientists have hypothesized that a bubble of warmer ice periodically travels up to the crust and repaves it, explaining the quirky heat behavior and intriguing surface features of this region.



The Cassini probe launched in 1997 and arrived at Saturn in 2004, where it dropped the European Huygens probe on the cloudy surface of the planet's largest moon Titan. Cassini was slated to be decommissioned in September of this year, but has received an extended mission that now runs through 2017.



The Cassini-Huygens mission is a joint project of NASA, the European Space Agency and the Italian Space Agency. It is managed by NASA's Jet Propulsion Laboratory in Pasadena, Calif.



Images — The Rings and Moons of Saturn

Cassini's Latest Discoveries

Special Report: Cassini's Mission to Saturn

Calculating the Positions of Planets

How to Calculate the Positions of the Planets: An Overview

from David Colarusso.com



This brief explanation describes the methods used in the simulation above to determine the Right Ascension (RA) and Declination (Dec) of the Sun, Mercury, Venus, Mars, Jupiter, and Saturn. It assumes some background in astronomy. However, there is a reasonably verbose glossary linked to what may be unfamiliar terms. In truth, this explanation is more for those wishing to know exactly what assumptions underlie the above simulation. However, this explanation does serve as a good case study in how to determine the planets' positions.



The simulation overlays the RA and Dec of the five planets visible to the naked eye and the sun atop an cylindrical projection of the Earth's sky. The name planet roughly translates to "wanderer." Knowing the geocentric model held for so long, many of my students simply assume the planets move about the sky in much the same manner as the moon or sun--steadily creeping eastward. They do not, and I developed this simulation to illustrate their true wandering nature.



Solving Kepler's Equation & Calculating Ephemerides



When first approaching this problem, I knew that I would need to solve Kepler's Equation and have a little fun with reference frames. I was surprised by the explanations available on the web. Most of them fell short of what I was looking for. They were either strictly qualitative or, if quantitative, unnecessarily opaque. This resulted mostly from having too few or poorly executed diagrams and illustrations. There were a few notable exceptions, and I have cited them in the references section. As I never formally studied celestial mechanics, these sources were my teachers and greatly helped acquaint me with the problem and its solutions. What I've attempted to do here is to weave together a relatively cogent "How to" on the solving of Kepler's Equation and the calculation of planetary positions in the Earth's sky.



Johannes Kepler (1571-1630) was a mathematician, astronomer, and Copernican. He believed that the Sun, not the Earth, lay at the center of the universe. He refined Copernicus's view of a heliocentric (Sun-centered) universe, making it into more than simply a competing theory for the geocentric (Earth-centered) model. Under Kepler it would become the superior predictive model. In his work Kepler formulated three laws of planetary motion first set down together in Harmonice Mundi (Harmonies of the World), 1618, and here they are.





Kepler's Laws:



1. The planets orbit about the Sun in elliptical orbits with the sun centered at one of the ellipse's two foci (Figure 1).

2. An imaginary line connecting the sun and a planet sweeps out equal areas in equal times as the planet moves through its orbit. A consequence of this is that a planet moves fastest when closest to the Sun. Newton will have something to say about this.



3. The square of the period of a planet's orbit is proportional to its distance from the Sun cubed. When the units used for distance are Astronomical Units (AU) and time is measured in years, this relationship can be written explicitly as an equation relating the planet's period P and the semi-major axis of its orbit a (eq.1).

Kepler's Laws meant that given only a handful of orbital parameters, one could say where a planet had been and would be. To state this explicitly, astronomers make use of Kepler's Equation (eq.2).

Kepler's equation is a transcendental equation. This means there is no general solution. So to find the location of a planet at a time t, we must solve for that time using some numerical method. First let us work with what we have. NOTE: You may find it helpful to reference Figure 2 (pop-up) to help visualize some of the variables referenced here.



Only e is time independent. So we consult our orbital parameters for its value and then solve for the mean anomaly (eq.3), M in Kepler's Equation (eq.2). The mean anomaly is just the angle with the perihelion that the planet would have if the orbit was an ellipse with eccentricity = 0, i.e., a circle. We call the imaginary planet moving along such an orbit the mean planet. In such a case the planet would move with a velocity V = (2*PI)/Period .

As you can see, the mean anomaly is just the mean planet's velocity times the time elapsed since it was last at the perihelion.

We can now find the eccentric anomaly using some numerical method. This simulation makes use of successive approximation. Once we have a value for E with which we are happy, we can find the true anomaly (eq.4). The true anomaly is the ACTUAL angle between the perihelion and the planet.

From here it is a simple matter to find the planet's radial distance (eq.5) from the sun.

We now have the planet's polar coordinates (r, v) within the plane of its orbit such that the X axis points from the Sun towards the Perihelion, point P.

Now we find the Heliocentric Ecliptic coordinates (x, y, z) for the planet by converting from polar to cartesian coordinates and rotating the frame such that the X axis points towards the first point of Aries.

We then rotate the coordinates into Heliocentric Equatorial coordinates (X, Y, Z), making use the matrix below.

However, our display shows the positions of the planets from the Earth. So we need to switch our vantage point to that of a geocentric system. To do this we first repeat the above process, solving for the Earth's Heliocentric Equatorial coordinates. We want to know the Sun's Geocentric coordinates. So here we will approximate this as the inverse of Earth's heliocentric coordinates. This is the same method used to find the Sun's location for display. It is important to note, however, that this is just an approximation, as what we really find is not the location of the Earth but rather that of the Earth-Moon system's barycenter. This simplification is responsible for limiting the simulation's accuracy. Note: This is not an issue for the Build Your Own Solar System simulation for teachers as the hypothetical "Earth" has no moon in that simulation. We then add the Sun's geocentric coordinates to those of the heliocentric coordinates of our planet. This shifts the coordinates, giving us the Geocentric equatorial coordinates (xp, yp, zp) for the planet.

Having the planet's Geocentric coordinates, it is a simple matter to convert them into Right Ascension and Declination. Note: Watch you signs here; if you're not careful, it WILL get messy.

That's it. We can now solve for many discreet times and collect the data into tables to construct ephemerides. If you are interested in finding more accurate calculations for the planets' positions, consider buying a copy of the Astronomical Almanac from the US Naval Observatory or making use of JPL's Horizons system.


References & Further Reading:



1. To anyone interested in why it is the orbits of the planets are elliptical, I suggest finding a copy of D. & J. Goodstein's Feynman's Lost Lecture: The Motion of Planets Around the Sun. W. W. Norton & Company. New York, NY. 1996.



2. A copy of Kepler's Harmonice Mundi (Harmonies of the World) as well as many other ground breaking texts in astronomy have been compiled into one tome: Stephen Hawking's On The Shoulders of Giants: The Great Works of Physics and Astronomy. Running Press. Philadelphia. 2002.



3. For what I found to be the most rigorous on-line handling of this material, try Dr. J. B. Tatum's Celestial Mechanics: http://orca.phys.uvic.ca/~tatum/celmechs.html (Link current as of April 2004).



4. The orbital parameters used here came from the JPL Solar System Dynamics Group's "Planetary Orbital Elements," JPL Solar System Dynamics: http://ssd.jpl.nasa.gov/elem_planets.html. (Link current as of April 2004).


Glossary of Terms



Ascending node: The point of intersection between a planet's orbit and the plane of the Sun's equator, where the planet is moving northward ("upward") across the plane of the Sun's equator.



Astronomical Units (AU): A measure of distance where one AU is just about equal to the average distance of the Earth from the Sun, 1.49597870691 x 108 (± 3) kilometers.



Barycenter: The center of mass for a multi-body system of mutually orbiting bodies. The system orbits about the barycenter.



Celestial sphere: A gigantic imaginary sphere surrounding a stationary Earth upon which the stars are affixed. It was once believed that the celestial sphere was real. However, it is now regarded solely as a convenient descriptive tool.



Celestial equator: The projection of the Earth's equator onto the celestial sphere.



Copernican: One who subscribes to the Copernican world view of a heliocentric universe, i.e., one who believes that the Earth orbits around a fixed Sun.



Declination (DEC): A heavenly object's position in the sky as measured along a meridian in degrees (0 to 90 degrees) north (+) or south (-) from the equator.

Descending node: The point of intersection between a planet's orbit and the plane of the Sun's equator, where the planet is moving southward ("downward") across the plane of the Sun's equator.



Eccentric Anomaly: a time dependent term in Kepler's equation which must be solved for in order to calculate a planet's position on its orbit.



Eccentricity: A measure of how "elliptical" an eclipse is (measured from 0 to 1). For example, a circle has an eccentricity of zero, not very elliptical. A relationship can be stated mathematically between the semi-major axis a, the semi-minor axis b and the eccentricity e where:

Above are four ellipses with varying eccentricities. The first is a circle.



Ecliptic: As seen from the Earth the ecliptic is the Sun's annual path across the sky.



Ephemerides: plural of ephemeris. Tables containing the calculated positions (usually RA and DEC) of celestial objects for different times, usually at regular intervals.



Ellipse: One of the conic sections, those shapes which are the intersection of a cone and plane. The ellipse is a geometric shape that looks like a squashed circle. You can easily make an ellipse with two thumb tacks and a loop of string. Place the two tacks into a paper and loop the string around them. Place a pencil in the loop of string and move it outwards until the loop becomes taut. Move the pencil around the tacks always keeping the slack out of the loop. The figure drawn is an ellipse. The points where the thumbtacks lie are the foci of the ellipse (singular focus).

Elliptical: Shaped like an ellipse.



First point of Aries: The position against the background stars of the Earth's descending node as seen from the Sun.



Foci: Plural of focus. See ellipse.



Geocentric: Earth centered.



Geocentric equatorial coordinates: An X,Y,Z coordinate system centered on the Earth in which the Earth's equator lies in the X-Y plane.



Heliocentric: Sun centered.



Heliocentric ecliptic cartesian coordinates: An X,Y,Z coordinate system centered on the Sun in which the ecliptic lies in the X-Y plane.



Heliocentric equatorial cartesian coordinates: An X,Y,Z coordinate system centered on the Sun in which the Sun's equator lies in the X-Y plane.



Kepler's Equation: An equation derived from Kepler's Laws whose solution can specify the position of a planet in its orbit for a specified time given a set of orbital parameters.

Mean anomaly: The angle between the perihelion and the mean planet as measured in the plane of its orbit.

Mean planet: An imaginary planet which moves at a constant velocity around a circular orbit with a radius equal to the semi-major axis of the actual planet's orbit.



Numerical method: A method for solving mathematics problems, usually by computer, through the repeated use of simple arithmetic operations.



Orbital parameters: A set of physical parameters for the orbit of a planet sufficient to predict the position of the planet at a given time t. The orbital parameters used in the simulation above can be found at: http://ssd.jpl.nasa.gov/elem_planets.html (valid as of June 2004).



Perihelion: The closest point on a planet's orbit to the Sun.



Period (of a planet): The length of time it takes a planet to return to the same place in its orbit.



PI (): The ratio of a circle's circumference C to its diameter D.

Polar Coordinates: A means of denoting a point's location by use of its radial distance from the origin and the angle it is from the x axis.



Radial distance: How far something is from the coordinate axes as measured directly out from the axes.



Retrograde Motion: The westward motion of the planets against the background stars. In order to maintain the Earth's central location and a commitment to perfect circular motion, geocentrists devised a set of epicycles (orbits within orbits) upon which the planets would rotate. The motion of the planet about its epicycle allowed for the presence of retrograde motion. However, heliocentrists' Sun-centered model had no need for epicycles as retrograde motion could bee seen as one planet simply overtaking another as they raced about the Sun. See Animation.



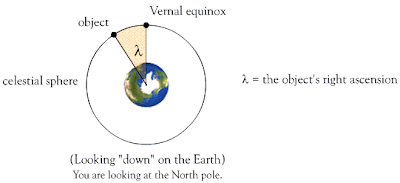
Right Ascension (RA): A heavenly object's position in the sky as measured in hours:minutes:seconds east (+) or west (-) from the vernal equinox.

Semi-major axis: See ellipse.



Semi-minor axis: See ellipse.



Successive approximation: A numerical method by which a solution is found to an equation by substituting in guesses for the answer on both sides of the equation. The sides are evaluated and the first guess that produces a difference between the sides of less than a pre-defined tolerance is taken to be the answer.



Sol: our sun.



Transcendental equation: An equation for which a general solution cannot be found algebraically as it contains transcendental (non-algebraic) functions.



True Anomaly: The angle between the perihelion and the planet as measured in the plane of its orbit.



Vector: A quantity consisting of both direction and magnitude (e.g., velocity).



Velocity: A measure of an object's motion that includes both the object's speed and direction.



Vernal equinox: Both the date (around March 21st) on which the Sun crosses the celestial equator moving northward and the point against the background stars where this occurs.


www.davidcolarusso.com